
Set - 집합
배열과 비슷하지만 많이 다른 자료 구조인 집합을 한번 봐보자.
집합은 중복을 허용하지 않는 자료구조다.
중복을 허용하지 않는 다는 말은 말 그대로 중복값을 반영 하지 않는다는 말과 같다. 실제로 집합의 종류는 다양하지만 이 게시글에선 배열 기반 집합만을 다룰 것이다.
배열 기반 집합과 일반 배열과의 유일한 차이점은 바로 중복값을 허용하지 않는다는 것이다.
다시말하면 집합은 중복을 허용하지 않는다는 간단한 제약을 받는 배열이다.
하지만 이런 제약으로 인해 실제로 앞서 설명한 네 연산중 하나에서 집합의 효율성이 매우 달라진다. 이런 배열 기반 집합으로 읽기, 검색, 삽입, 삭제 연산을 수행해 보자!
읽기📃
먼저 읽기 부분은 배열 읽기와 완전히 똑같다. 컴퓨터가 특정 인덱스에 들어 있는 값을 찾는 데 한 단계면 가능하다. 왜냐면 이전에 배열 부분에서 설명한 대로 컴퓨터는 집합이 시작하는 메모리 주소를 알고 있으므로 집합안에 어디든(인덱스) 갈 수 있다.
검색🔎
검색도 마찬가지로 배열과 별반 차이점이 딱히 없다. 어떤 값이 집합 내에 존재하는지 알려면 검색에 최대 N단계까지 걸릴 수 있다.
삭제✂
삭제도 마찬가지로 배열과 집합에서 동일하다. 값을 삭제하고 빈 공간을 매꾸기 위해 N단계를 거쳐 데이터를 왼쪽으로 옮긴다.
삽입🎬
하지만 삽입은 다르다
배열에서 최선의 시나리오였던 집합의 맨 끝에 삽입하는 방법을 먼저 한번 생각해보자. 먼저 배열에서는 컴퓨터가 1단계로 값을 끝에 삽입했던 것이 기억나는가?

하지만 집합에서는 먼저 이 값이 이미 집합에 들어 있는지 결정해야 한다.
그러니까 중복 데이터를 막는 게 바로 집합의 역할이기 때문에 이런 동작을 하는 것이다. 따라서 모든 삽입에는 검색이 우선적으로 동작한다.
array = ["진로", "카스", "테라", "위스키"]배열때 설명했던 쇼핑 리스트를 다시 불러왔다.
여기서 만약 "진"을 추가 하려면 먼저 이것이 이미 있는지 검색을 한번 수행한 후 다음의 단계를 거쳐야 한다.
집합에서 삽입의 단계
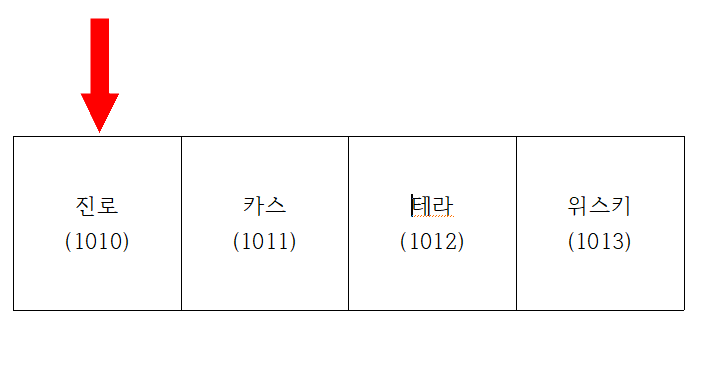
- 인덱스 0에서 "진"을 검색한다. 만약 없다면(아니라면) 다음 인덱스로 넘어가 이 작업을 반복한다.
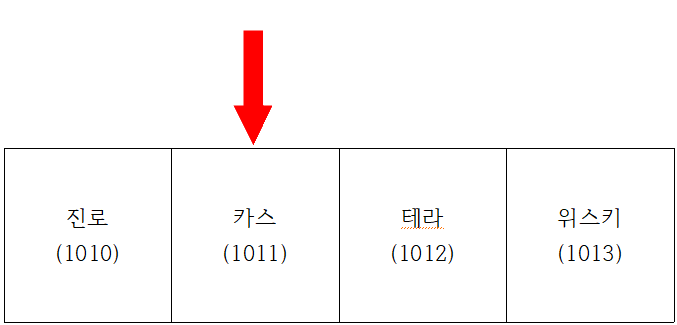
- 인덱스 1에서 "진"을 검색한다.
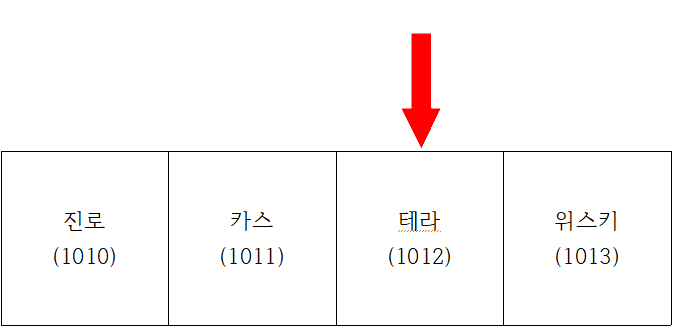
- 인덱스 2에서 "진"을 검색한다.
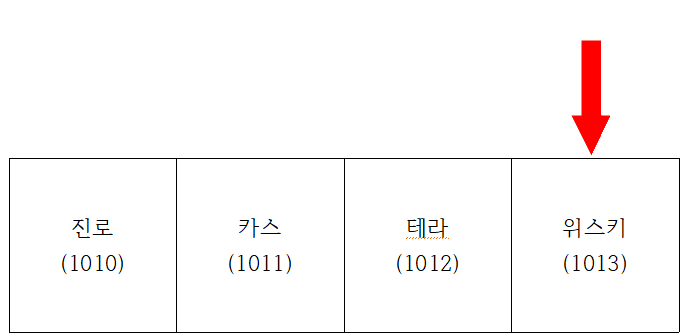
- 인덱스 3에서 "진"을 검색한다.
이제 집합을 전부 검사한결과 "진"이라는 값이 중복되지 않았으니 마지막 단계가 남았다.

- 셀을 하나 추가해 "진"이라는 값을 추가한다.
집합의 끝에 값을 삽입하는게 가장 최선의 시나리오인데도 무려 5단계 연산을 수행해야 했다. 그러니 최종 삽입 단계를 수행하기 전에 4개의 원솔르 모두 검사했다느 말과 같다.
정리하자면 집합 삽입에서 최선의 시나리오에는 원소 N개에 대해 N+1단계가 필요하다는 말이다.
- 값이 집합에 없음을 확인하는데 N단계의 검색을...
- 이어서 실제 삽입에 1단계를 사용 하니 총 N+1이다.
최악의 시나리오에는? 😫😑
만약 값을 삽입하는 셀이 맨 앞이라는 최악의 시나리오라면 컴퓨터는 셀 N개를 전부 검색해서 집합에 중복 값의 유무를 파악하고 또 다른 N단계로 모든 데이터를 오른쪽으로 옮겨야 하며 마지막 단계에서는 새 값을 삽입해야한다. 그러니 총 2N+1단계로 볼 수 있다.
배열보다 집합이 불리한가?😣
그렇진 않다. 집합의 특성을 이용하는 상황이 온다면 집합을 사용하는 것이 당연하다.
(중복된 값이 없어야 할 경우)
하지만 이런 특수한 요구 사항이 없을 경우 집합 삽입 보다 배열 삽입이 더 효율적이므로 배열이 나을 수 있다. 그래서 요구 사항을 먼저 확인 한 후에 알맞는 자료 구조를 선택하는 것을 연습해놓자.
'할머니도 이해하는 자료구조, 알고리즘' 카테고리의 다른 글
| 6. 정렬(sort) (0) | 2022.08.02 |
|---|---|
| 5. 알고리즘이 중요한 이유 (0) | 2022.08.02 |
| 3. 배열 (0) | 2022.08.02 |
| 1. 인트로 (0) | 2022.08.02 |








