
정렬된 배열
이 뜻은 배열과 거의 같다. 유일한 차이는 값이 항상 순서대로있어야 한다는 것에서 다르다!
그러니까 값을 추가할 때마다 적절한 셀에 넣어 배열의 값을 정렬된 상태로 유지한다.
하지만 배열은 이것과 달리 값의 순서는 고려하지 않고 배열의 끝에 값을 추가 할 수 있다.

여기서 75를 일반적인 배열에 삽입한다고 가정하면 아래와 같이 된다.

배열 파트에서 설명 했듯이 컴퓨터는 맨 끝에 삽입하는 것이라면 한 단계만에 처리 할 수 있다.
하지만 정렬된 배열에서는 값을 오름차순으로 유지하려면 적절한 위치에 75를 삽입해야 한다.

위에 그림 처럼 75를 알맞는 위치에 넣기 위해선 한 단계로는 부족하다 먼저 75가 들어갈 올바른 위치를 찾는 것이 먼저고 이후 다른 값들을 옮기는 작업을 해야한다. 그러면 단계적으로 살펴보자!
75를 삽입해보자

처음배열은 이렇게 됐었다. 그리고 이제 75를 넣고 오름차순으로 유지시켜야 한다.
- 1단계: 인덱스 0 의 값을 확인해서 삽입하려는 값인 75가 왼쪽으로 들어갈지 오른쪽으로 갈지 정해야한다.

75는 3보단 크니까 오른쪽 어딘가에 삽입해야 함을 알 수 있다. 하지만 정확히 어떤 셀에 들어가야 할지 아직은 모르니 다음 셀을 확인해보자.
- 2단계: 다음 셀의 값을 확인한다.

75는 17보단 크니까 오른쪽 어딘가에 삽입해야 한다. 그리고 다시 다음 값을 확인한다.
- 3단계: 다음 셀의 값을 확인한다.

드디어 75보다 큰 값이 나왔다. 정렬된 배열을 유지하려면 80바로 왼쪽에 75를 넣어야 한다고 판단이 가능하다. 하지만 이제 삽입을 하려면 셀을 하나 가져오고 나머지 값들을 모두 옮겨야 한다.
- 4단계: 마지막 값을 오른쪽으로 옮긴다.

- 5단계: 마지막 앞에 있던 값을 오른쪽으로 옮긴다.

- 6단계: 이제 75를 삽입한다.

드디어 끝났다!
정렬된 배열에 삽입할 때는 항사 실제 삽입 전에 검색을 먼저 한다.
그런 다음 삽입할 올바른 위치를 정해야 한다. 이게 바로 배열과 정렬된 배열의 주된 차이점 중 하나다.
삽입에 있어 정렬된 배열이 일반 배열보다 덜 효율적이나 정렬된 배열은 검색 연산에 강하다!
정렬된 배열의 검색🔎
먼저 검색이라 함은 배열 부분에서 원하는 값을 찾을 때까지 처음 부터 끝까지 하나하나 찾는 것이라 했다. 그리고 이것을 선형 검색이라고 부른다고 했다.
아무래도 정렬된 배열에서 선형 검색을 하는 것이 그냥 배열에서 하는 것 보단 훤씬 효율 적일 수 있다.
일반적인 배열 vs 정렬된 배열 🤔
[1, 2, 3, 4, 5, 7, 10, 23, 0] 이런 배열이 있다고 쳐보자.
- 만약 22를 찾을껀데 일반적인 배열이라면 처음 부터 끝까지 찾을 것이다.
- 하지만 정렬된 배열이라면 값이 배열에 없을때 검색을 더 빨리 멈 출수 있다.
- 코드를 22이상 부터는 검색을 하지 않겠다고 만들면 된다.
간단하게 생각을 해봐도 선형 검색에선 일반적 배열보단 정렬된 배열이 더 유리하다. 그리고 이 선형 검색은 가능한 알고리즘 중 하나 일뿐 이것만이 존재하는 것은 아니다!
선형 검색은 원하는 값을 검색하는 데 사용 할 수 있는 여러 가지 중 하나일 뿐이다.
정렬된 배열이 일반적 배열보다 더 큰 장점은 다른 검색 알고리즘을 쓸 수 있다는 것이다.
이런 알고리즘을 이진 검색(Binary search)라고 부르는데 이진 검색은 선형 검색 보다 훨씬 빠르다!
이진 검색
if 조건문을 공부할때 예시로 많이 나오는 UP and DOWN 게임이 이진 검색이라 생각하면 편하다.
1 부터 100까지 생각한 숫자를 맞춰봐
이렇게 나온다면 먼저 50을 고르면 된다. 그러면 UP 혹은 DOWN 둘중 하나가 나올태니 적어도 반은 검색에서 제거 할 수있다. 이것이 이진 검색이다. 정렬된 배열은 이런 이진 검색을 할 수 있다. 일반적 배열은 할 수 없다.
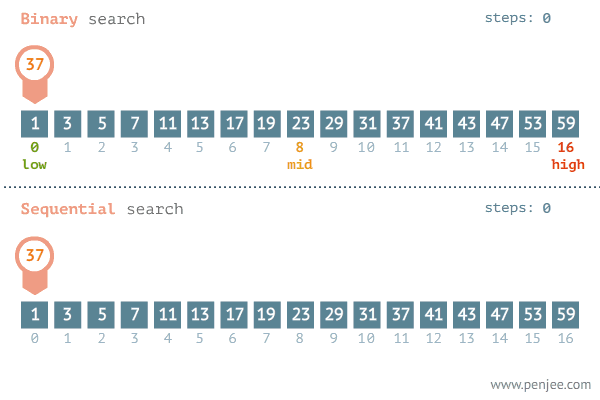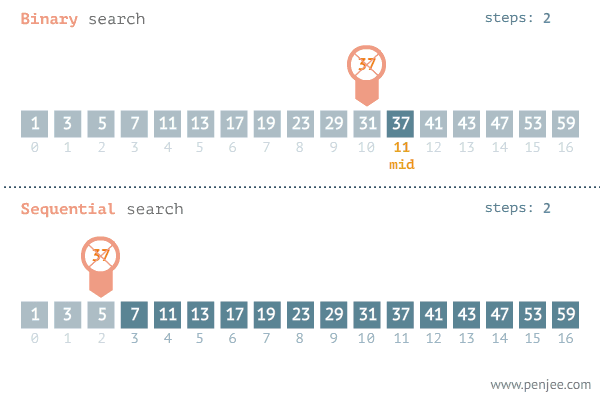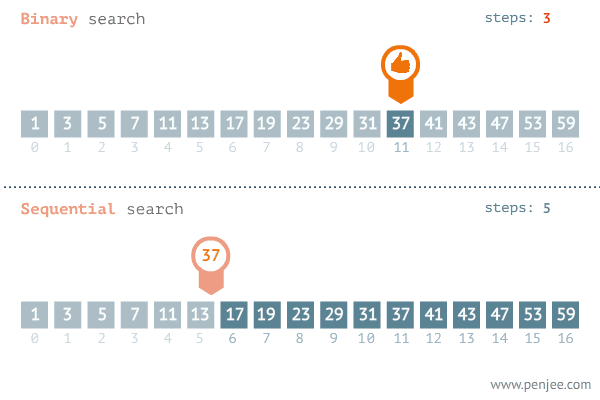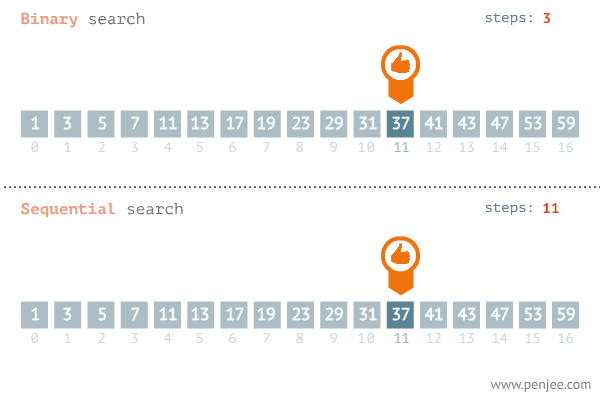
이제 배열로 확인해보자
원소 9개를 포함하는 정렬된 배열이 있습니다.

컴퓨터는 각 셀에 어떤 값이 있는지 모르니까 다음과 같이 배열을 묘사 한다. 여기서 만약 값 7을 찾는다고 해보고 이진 검색으로 찾아보자.
- 1단계: 가운데 셀부터 검색을 시작한다! 배열의 길이를 알고 있으니 가운데 셀에 접근하기 쉽고 길이를 2로 나누면 적절한 메모리 주소로 바로 이동이 가능하다.

- 2단계: 가운데 값이 9로 드러났으므로 7을 찾아야하니 가운데 보다 오른쪽에 있는 값들은 전부 제외한다. 그리고 9보다 왼쪽에 아무곳 한곳을 확인해보자


두번째 값이 4로 드러났고 7보다는 작으니 두번째 값을 포함해 왼쪽에 있는 값들을 모두 제외하자.
이제 남은것은 세번째와 네번째 값만이 남았다.
- 3단계: 두 셀중 임의로 왼쪽 셀을 선택한다.

- 4단계: 마지막 남은 셀을 확인한다 만약 여기에 7이 없다면 이 정렬된 배열에는 7이 없다는 것을 의미한다.

이렇게 4단계만에 7을 찾을 수 있었다. 스위프트로 구현해보면?
- 재귀함수로 구현
func binary_search(_ array:[Int], value: Int) -> Bool {
if array.count == 1{
return array[0] == value ? true : false
}
let mid = array.count / 2
let range = array[mid] > value ? (0..<mid) : ((mid + 1)..<array.count)
return binary_search(Array(array[range]), value: value)
}- 반복문으로 구현
func binary_search(_ array: [Int], num: Int) -> Bool {
var start = 0
var end = (array.count - 1)
// 먼저 찾으려는 값이 있을 수 있는 상한선과 하한선을 정한다
// 최초의 상한선은 배열의 첫 번째 값 그리고 하한선은 마지막 값이다.
// 상한선과 하한선 사이에 가운데 값을 계속 해서 확인하는 루프를 시작한다.
while start <= end {
// 상한선과 하한선 사이에 중간 지점을 찾는다.
let mid = (start + end) / 2
// 중간 지점의 값을 확인한다.
if array[mid] == num {return true}
// 중간 지점의 값이 찾고 있던 값이면 검색을 끝낸다.
// 그렇지 않다면 더 클지 작을지 추측한 바에 따라 상한선이나 하한선을 바꾼다.
if array[mid] > num {
end = mid -1
} else {
start = mid + 1
}
}
// 상한선과 하한선이 같아질 때 가지 경곗값을 줄였다면
// 찾고 있는 값이 이 배열에 없다는 의미다.
return false
}코드는 스위프트를 사용해서 구현하였다.
마무리.
이진검색 vs 선형 검색
먼저 그래프를 보자.

작은 크기의 배열이라면 사실 두 검색 방법은 크게 상관이 없다. 하지만 배열이 커진다면 이야기는 달라진다.
100개의 값을 갖는 배열에서 각 검색에 필요한 최대 단계 수는 다음과 같다.
- 선형 : 100단계
- 이진 : 7단계
압도적인 차이다.
그래프를 보면 알겠지만 원소수가 늘어나면 늘어날 수록 선형 검색은 그것과 똑같이 늘어나지만 이진 검색은 차이점이 별로 없다. 실제로 백만개의 원소가 있다면 이진 검색은 단 20단계면 찾을 수 있다.
강조 & 마무리
강조하지만 정렬된 배열이 무조건 모든 상황에서 빠른것은 아니다! 앞서 봤듯이 정렬된 배열의 삽입은 일반 배열보다 느리다! 하지만 장단점이 있다.
- 정렬된 배열의 삽입은 일반 배열보단 느리지만 검색은 훨씬 빠르다.
다음에는 빅 오 표기법과 시간복잡도를 다룰 예정이다.
이미지 출처는 서적 A Common-Sense Guide to Data Structures and Algorithms: Level Up Your Core Programming Skills 에서 따왔다.
'할머니도 이해하는 자료구조, 알고리즘' 카테고리의 다른 글
| 5. 알고리즘이 중요한 이유 (0) | 2022.08.02 |
|---|---|
| 4. 집합 (0) | 2022.08.02 |
| 3. 배열 (0) | 2022.08.02 |
| 1. 인트로 (0) | 2022.08.02 |








